Author: Ed Nelson
Department of Sociology M/S SS97
California State University, Fresno
Fresno, CA 93740
Email: ednelson@csufresno.edu
Note to the Instructor: The data set used in this exercise is gss14_subset_for_classes_STATISTICS.sav which is a subset of the 2014 General Social Survey. Some of the variables in the GSS have been recoded to make them easier to use and some new variables have been created. The data have been weighted according to the instructions from the National Opinion Research Center. This exercise uses FREQUENCIES in SPSS to explore measures of skewness and kurtosis. A good reference on using SPSS is SPSS for Windows Version 23.0 A Basic Tutorial by Linda Fiddler, John Korey, Edward Nelson (Editor), and Elizabeth Nelson. The online version of the book is on the Social Science Research and Instructional Council's Website. You have permission to use this exercise and to revise it to fit your needs. Please send a copy of any revision to the author. Included with this exercise (as separate files) are more detailed notes to the instructors, the SPSS syntax necessary to carry out the exercise (SPSS syntax file), and the SPSS output for the exercise (SPSS output file). Please contact the author for additional information.
I’m attaching the following files.
- Data subset (.sav format)
- Extended notes for instructors (MS Word; docx format).
- Syntax file (.sps format)
- Output file (.spv format)
- This page (MS Word;
Goals of Exercise
The goal of this exercise is to explore measures of skewness and kurtosis. The exercise also gives you practice in using FREQUENCIES in SPSS.
Part I – Measures of Skewness
A normal distribution is a unimodal (i.e., single peak) distribution that is perfectly symmetrical. In a normal distribution the mean, median, and mode are all equal. Here’s a graph showing what a normal distribution looks like.
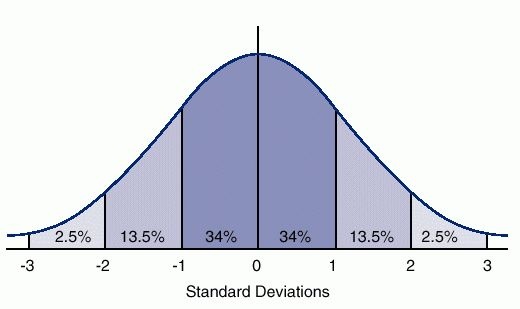
The horizontal axis is marked off in terms of standard scores where a standard score tells us how many standard deviations a value is from the mean of the normal distribution. So a standard score of +1 is one standard deviation above the mean and a standard score of -1 is one standard deviation below the mean. The percents tell us the percent of cases that you would expect between the mean and a particular standard score if the distribution was perfectly normal. You would expect to find approximately 34% of the cases between the mean and a standard score of +1 or -1. In a normal distribution, the mean, median, and mode are all equal and are at the center of the distribution. So the mean always has a standard score of zero.
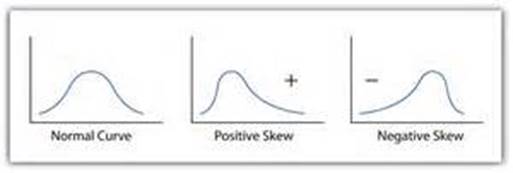
Skewness measures the deviation of a particular distribution from this symmetrical pattern. In a skewed distribution one side has longer or fatter tails than the other side. If the longer tail is to the left, then it is called a negatively skewed distribution. If the longer tail is to the right, then it is called a positively skewed distribution. One way to remember this is to recall that any value to the left of zero is negative and any value to the right of zero is positive. Here are graphs of positively and negatively skewed distributions compared to a normal distribution.
The best way to determine the skewness of a distribution is to tell SPSS to give you a histogram along with the mean and median. SPSS will also compute a measure of skewness. Run FREQUENCIES in SPSS for the variables d1_age and d9_sibs. (See Frequencies in Chapter 4 of the online SPSS book mentioned on page 1.) Click on the “Charts” button and select “Histogram” and “Show normal curve on histogram.” Then click on “Continue.” Now click on “Statistics” and select mean, median, skewness and kurtosis. Then click on “Continue” and on “OK.” We’ll talk about kurtosis in a little bit.
Notice that the mean is larger than the median for both variables. This means that the distribution is positively skewed. But also notice that the mean for d9_sibs is quite a bit larger than the median in a relative sense than is the case for d1_age. This suggests that the distribution for d9_sibs is the more skewed of the two variables. Look at the histograms and you’ll see the same thing. Both variables are positively skewed but d9_sibs is the more skewed variable. Now look at the skewness values — 1.726 for d9_sibs and .244 for d1_age. The larger the skewness value, the more skewed the distribution. Positive skewness values indicate a positive skew and negative values indicate a negative skew. There are various rules of thumb suggested for what constitutes a lot of skew but for our purposes we’ll just say that the larger the value, the more the skewness and the sign of the value indicates the direction of the skew.
Run FREQUENCIES for the following variables. Tell SPSS to give you the histogram and to show the normal curve on the histogram. Also ask for the mean, median, and skewness. Write a paragraph for each variable explaining what these statistics tell you about the skewness of the variables.
- d20_hrsrelax
- tv1_tvhours
Part II – Measures of Kurtosis
Kurtosis refers to the flatness or peakness of a distribution relative to that of a normal distribution. Distributions that are flatter than a normal distribution are called platykurtic and distributions that are more peaked are called leptokurtic.
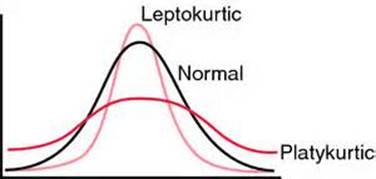
SPSS will compute a kurtosis measure. Negative values indicate a platykurtic distribution and positive values indicate a leptokurtic distribution. The larger the kurtosis value, the more peaked or flat the distribution is.
Look back at the output for d1_age and d9_sibs. For d1_age the kurtosis value was -.798 indicating a flatter distribution and for d9_sibs kurtosis was 4.409 indicating a more peaked distribution. To see this visually look at your histograms.
Run FREQUENCIES for the following variables. Tell SPSS to give you the histogram and to show the normal curve on the histogram. Also ask for kurtosis. Write a paragraph for each variable explaining what these statistics tell you about the kurtosis of the variables.
- d22_maeduc
- d24_paeduc
- s6_sexfreq


